<SVM> サポートベクタマシン自主勉強(1):方針
ちょっと間が空いてしまいましたが機械学習のエントリとなります。前回最後にちらっとお話ししたのですが、サポートベクタマシン(SVM)に足を突っ込んでみたいと思っています。
SVMのコーディングが自力でできない問題
ただ、このSVMは何回か挑戦して失敗している経緯があります。前回のようにはじパタ本だけでは私のレベルでクリアができない代物となります。そこではじパタと合わせて、「異常検知と変化検知」の内容と相互補完してみています。

- 作者: 井手剛,杉山将
- 出版社/メーカー: 講談社
- 発売日: 2015/08/08
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る
そこでやっと、SVMの概要について理解した。。。。つもりでした。しかしながらいざこれをスクリプトに落とそうとするとどう書いていいのかわからない。つまりロジックがわかったつもりでも、実行に移すとなるとどうしていいのかわからなくなってしまいました。
頼るべきはGoogle先生と集合知
しかしながらもうすでに歴史のあるこの分野では検索してしまえばいくらでもコードが出てきます。今回は以下のサイトさまのコードを拝借してやはりアヤメデータを使った分類を行ってみました。
こちらのコードは の線形で分離をして
を1, -1とわけています。アヤメデータもとりあえず、3種のうちの最初の1種を1, その他を-1としてインプットするコードに改造をしてみました。
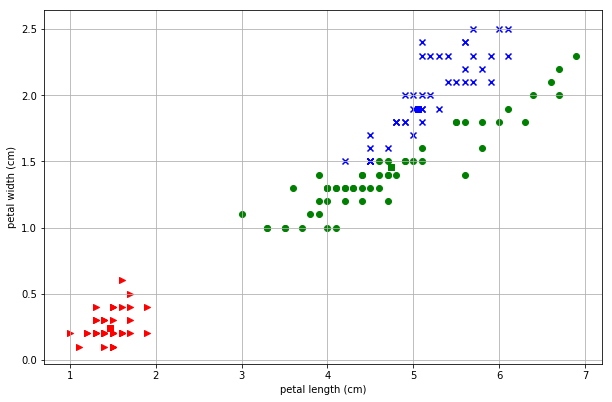
その結果が以下となります。
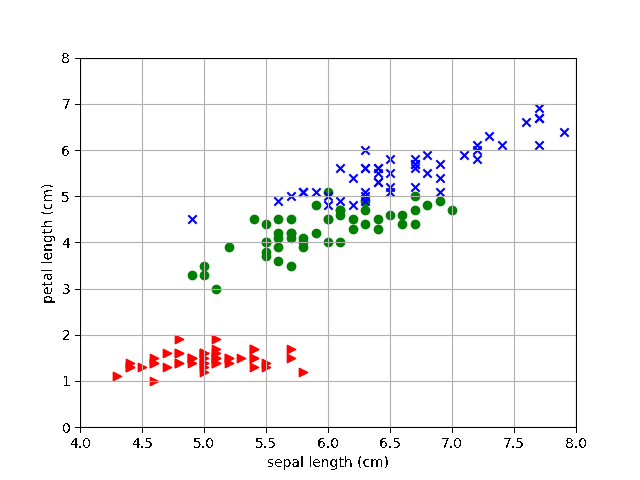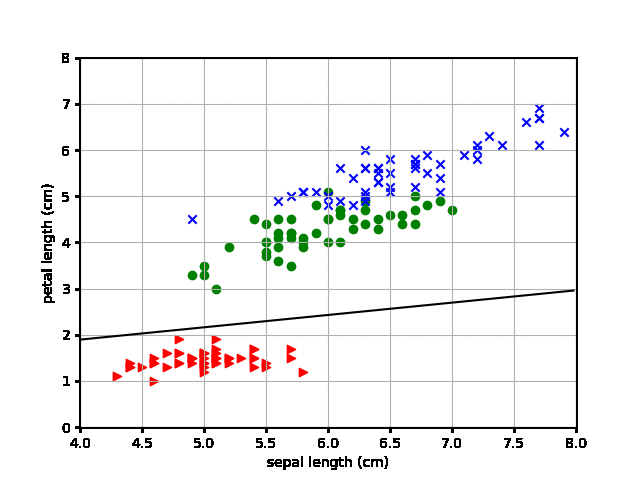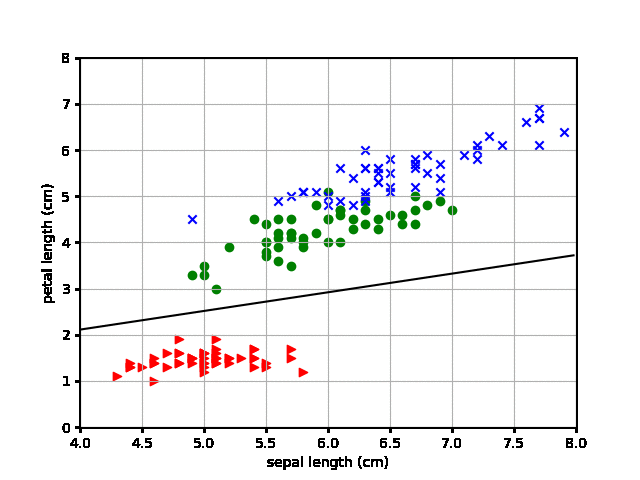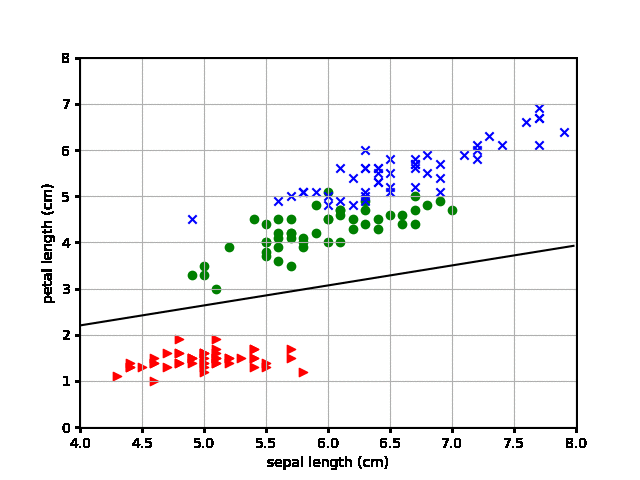
おぉ、なんとなく分類する線が学習を経るごとに赤と緑の間にはいっていきますね。赤が1としたアヤメデータなのでうまくいっているようです。
ここからスタート
SVMについてまとめることはたくさんありそうです。ラグランジュ乗数法、正則化、双対問題、KKT条件、カーネルトリック。数学的要素が多くどこまでカバーできるかわかりませんが、まず次回はこのスクリプトについて解いていくことから初めてみようかと思います。正直きちんと着地できるかまだ不明瞭ではあります。
コード
Jupyter Notebookで実行しています。
import sys import numpy as np from sklearn import datasets import itertools import matplotlib.pyplot as plt #inline pyplot from matplotlib import animation from IPython.display import HTML iris = datasets.load_iris() features = iris.data feature_names = iris.feature_names targets = iris.target class SVM(): def __init__(self, v1=0, v2=2, t=0): self.X = np.array([features.T[v1], features.T[v2]]).T self.T = np.array([1 if i==t else -1 for i in targets]) self.N = self.X.shape[0] self.d = self.X.shape[1] self.alpha = np.zeros(self.N) self.beta = 1.0 self.eta_al = 0.0001 self.eta_be = 0.1 self.v = [v1, v2] def test(self): print(self.X.shape) print(self.T) print(self.N) print(self.alpha) def plot_map(self, w, b): plt.subplot(1, 1, 1) seq = np.arange(4.0, 8.0, 0.02) plt.xlabel(feature_names[self.v[0]]) plt.ylabel(feature_names[self.v[1]]) plt.xlim(4, 8) plt.ylim(0, 8) plt.plot(seq, -(w[0] * seq + b) / w[1], 'k-') #plt.autoscale() plt.grid() for t, marker, c in zip(range(3), '>ox', 'rgb'): #print(self.X[self.T==1], 0) #print(self.T) plt.scatter( features[targets == t, self.v[0]], features[targets == t, self.v[1]], marker=marker, c=c, ) #print(linear_pro(w, np.array([1.,1.,1.]))) plt.show() def rtin(self, show=False): k_w = np.array([-100.0, -100.0]) k_b = -100.0 value = [] for _itr in range(1000): for i in range(self.N): self.delta = 1 - (self.T[i] * self.X[i]).dot(self.alpha * self.T * self.X.T).sum() - self.beta * self.T[i] * self.alpha.dot(self.T) self.alpha[i] += self.eta_al * self.delta for i in range(self.N): self.beta += self.eta_be * self.alpha.dot(self.T) ** 2 / 2 index = self.alpha > 0 w = (self.alpha * self.T).T.dot(self.X) b = (self.T[index] - self.X[index].dot(w)).mean() value.append([w, b]) if (np.power(np.array([k_w - w]), 2) < 0.00001).all() and (k_b - b) ** 2 < 0.00001: print(_itr) break if _itr % 10 == 0 and show: self.plot_map(w, b) k_w = w k_b = b return value svm = SVM(t=0) _ = svm.rtin(True)
<はじパタ> おまけ:混合ガウスモデルの検証
前回の記事より。 bython-chogo.hatenablog.com
EMアルゴリズムの実装を行ってみたのですが、アヤメの2次元データではこの混合ガウスモデル、EMアルゴリズムはうまく適用できないね、という結論になりました。2つの山が重なったピーナッツを横にクラスタリングしてほしいのに、縦に割ってしまうようで、初期値をランダムにするとほとんどうまくいかにようでした。
でも、本当でしょうか。私のコードになにか問題があって、うまくクラスタリングができなかった可能性を排除しきれません。いや、むしろこんな超適当コードを信じられないのです。そうだ、私のコードが間違っていてちゃんとEMアルゴリズムの実装ができればうまくいくのではないか。
そんな疑念についてはっきりさせるために積読してあった以下の書籍に書かれているコードを改造して改めて同じデータのプロットをしてみました。

Pythonで学ぶあたらしい統計学の教科書 (AI & TECHNOLOGY)
- 作者: 馬場真哉
- 出版社/メーカー: 翔泳社
- 発売日: 2018/04/19
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
その結果が、こ・れ・だ
やっぱり縦に割ってるじゃねーか!
というわけでEMアルゴの実力はほかのデータセットで確認をしたほうがよさそうですね。次回ははじパタの11章ですが、もしかしたらサポートベクタマシンのほうに浮気するかもしれません。
<はじパタ> 10.4 確率モデルによるクラスタリング
はい、ここまで10章の教師なし学習のクラスタリングをやってまいりましたが、10章も最後となりました。とりあえず一章をきちんと走り抜けられてよかったです。 で、ここは前回までのK-平均法や融合法と違い、各要素がそれぞれのクラスに入る確率を求める確率モデルによるクラスタリングをおこないます。キーワードとしては、混合正規分布モデルとEMアルゴリズムとなるようです。わかりやすい説明はこちらのリンクをご参照、とりあえず自分なりにまとめてみます。
混合正規分布モデル
各クラスタの分布がそれぞれ正規分布にしたがうと仮定をしてその平均と分散が一番Fitする最尤の値を求めていくものになります。また、ある要素に関してそれぞれクラスタの割合を表現する混合比なる重みづけのためのパラメータもでてきてこの値もいじる必要があります。
EMアルゴリズム
所属しているクラスタを示す隠れ変数があるものとして、その変数の確率モデルの最尤推定値を求めるのに優れているのが、EMアルゴリズムとなるようです。E(Expectation)ステップで隠れ変数に対しての期待値を計算、M(Maximization)ステップでその隠れ変数の最大値を計算するようにします。
はじパタに限らず、いくつかの本にこのEMのステップで何が行われているかの数式や説明があるのですが、いかに示すサイトの説明が図として直感的に何をしているのかわかりやすく書かれていると思いました。こういうの貴重。
www.slideshare.net
ピーナッツを縦に割っちゃう問題
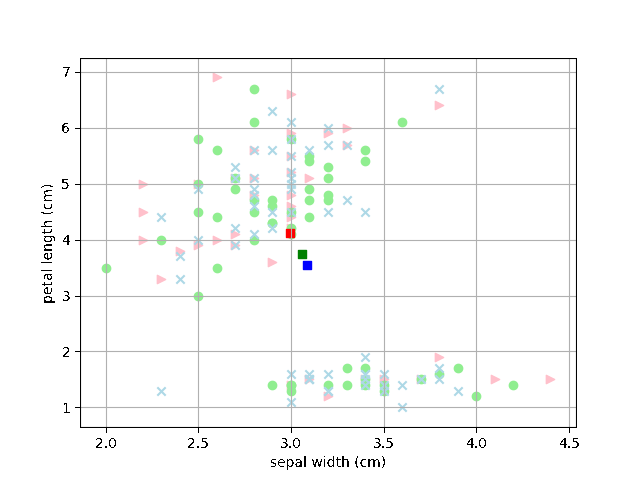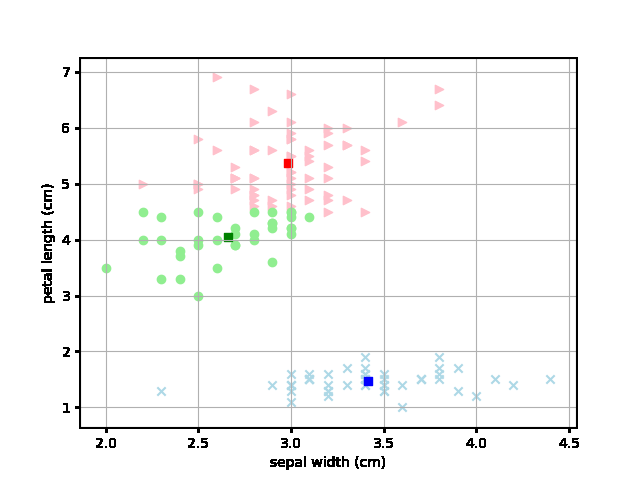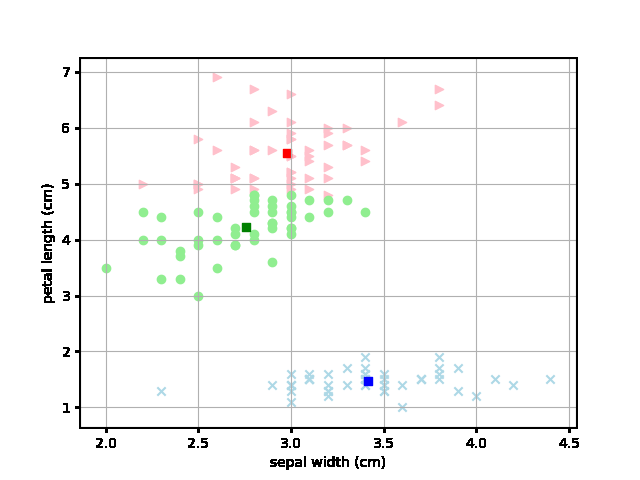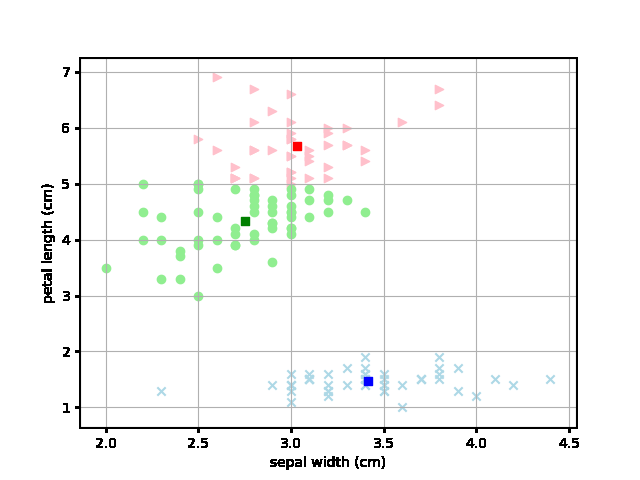
それで、コーディングを走らせてみたのですが、どうしても正解率が上がらないんです。実際にプロットをしてみると以下のように右上のピーナッツを縦にわるようなクラスタリングをしてしまうのです。

これは初期値にだいぶよるようですね。平均値のmuの値を意図的に変えてみたところ以下のようにピーナッツを横にわるような「理想的な」クラスタに収束することもあるようです。
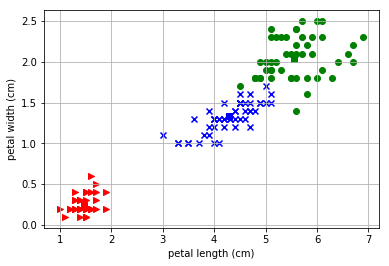
初期値をランダムに置くようにして確認してみましたが、この理想的な形状に収まるのは10回に1~2回程度のようです。
合わないモデル?
初期値問題に頭を抱えて機械学習のお師匠様のところに相談したところ、「そもそも合わないモデルだったのでは」とのことです。考察としてはアヤメデータ以外でもこのEMアルゴリズムを試してみてうまく当てはまるかを確認してみたほうが良いかもしれないです。やるかはわからないですが。
ソースコード
いつも以上にとっちらかったソースになってしまっていると思います。まあ備忘録なので。
import numpy as np from sklearn import datasets import itertools import matplotlib.pyplot as plt #inline pyplot iris = datasets.load_iris() features = iris.data feature_names = iris.feature_names targets = iris.target from collections import Counter class Iris_PModel: def __init__(self): self.p = [] self.x = [] self.y = [] self.t = [] self.pt = [] self.num = [50, 50, 50] iris = datasets.load_iris() features = iris.data targets = iris.target def install(self, a=2, b=3): self.x = features.T[a] self.y = features.T[b] self.t = targets self.pi = [1/3, 1/3, 1/3] self.means_dists() def plot_map(self, df=False): p = self.pt if df: p = self.t for t, marker, c in zip(range(3), '>ox', 'rgb'): plt.scatter( features[p == t, 2], features[p == t, 3], marker=marker, c=c, ) plt.scatter( self.mu[t][0], self.mu[t][1], marker='s', c=c ) plt.xlim(1.9, 4.5) plt.ylim(0.9, 7.1) plt.xlabel(feature_names[2]) plt.ylabel(feature_names[3]) plt.autoscale() plt.grid() plt.show() def randomize(self): self.pt = np.array([np.random.randint(3) for i in range(sum(self.num))]) def norm(self, mu, sigma): n_mu = np.array(mu) n_sig = np.array([[sigma[0], sigma[2]],[sigma[2], sigma[1]]]) n_det = np.linalg.det(n_sig) n_inv = np.linalg.inv(n_sig) nv = [] for i in range(150): n_c = np.array([self.x[i], self.y[i]]) - n_mu nv.append((1/(2*np.pi*np.sqrt(n_det))) * np.exp(- n_c.dot(n_inv).dot(n_c).T/2)) return(nv) def means_dists(self, init=True): if init: self.randomize() x_m = sum(self.x)/150 y_m = sum(self.y)/150 self.nu = [[np.random.normal(x_m, 1), np.random.normal(y_m, 1)], [np.random.normal(x_m, 1), np.random.normal(y_m, 1)], [np.random.normal(x_m, 1), np.random.normal(y_m, 1)]] print("mu", self.mu) self.v = [[1.0, 1.0, 0.0], [1.0, 1.0, 0.0], [1.0, 1.0, 0.0]] def m_step(self, gamma): n_k = [sum([gamma[i][j] for i in range(150)]) for j in range(3)] self.mu = [[sum([self.x[i]*gamma[i][j] for i in range(150)])/n_k[j], sum([self.y[i]*gamma[i][j] for i in range(150)])/n_k[j]] for j in range(3)] self.v = [[sum([(self.x[i]-self.mu[j][0])**2*gamma[i][j] for i in range(150)])/n_k[j], sum([(self.y[i]-self.mu[j][1])**2*gamma[i][j] for i in range(150)])/n_k[j], sum([(self.x[i]-self.mu[j][0])*(self.y[i]-self.mu[j][1])*gamma[i][j] for i in range(150)])/n_k[j]] for j in range(3)] self.pi = [n_k[i]/150 for i in range(3)] def e_step(self, init=False): if init: self.install(2, 3) nv = [self.norm( self.mu[i], self.v[i]) for i in range(3)] snv = [nv[0][i]*self.pi[0] + nv[1][i]*self.pi[1] + nv[2][i]*self.pi[2] for i in range(150)] prop = [[nv[0][i]*self.pi[0]/snv[i], nv[1][i]*self.pi[1]/snv[i], nv[2][i]*self.pi[2]/snv[i]] for i in range(150)] return prop def process(self): gamma = self.e_step(True) self.m_step(gamma) pre_result = [] for i in range(31): result = [] for g in gamma: result.append(g.index(max(g))) self.pt = np.array(result) max_int = [0, 0, 0] if pre_result == result: print(self.pi) self.plot_map() break pre_result = list(result) gamma = self.e_step(False) self.m_step(gamma) krs = Iris_PModel() krs.process()
<はじパタ> おまけ:共分散行列のコーディングに苦戦した話
今、はじパタのコーディングをせっせとやってはブログに上げているという作業を続けていますが、いかんせん付け焼刃の知識のために基本的と思われるところで引っかかってしまうことも、多く、今後の備忘録的にも失敗とリカバリの記録を残してみようと思います。
現象:NaNエラーが発生
10.4 「確率モデルによるクラスタリング」をやっていくと、EMモデルの繰り返しによって数値がNaNとなってしまう現象が発生。ひとつNaNがでてくるとその数値を使った値もNaNとなるので真賀田博士もびっくりのすべてがNaNになってしまうのでした。以下がその時のログ。
MU: [[4.2591681450807695, 1.3885253632923946], [3.3363395791482486, 1.0264189358663134], [3.6851362069583895, 1.1830943936011733]] V: [[2.8113007747631147, 2.9874538055910858, 3.042873375542265], [0.51266119363098883, 0.56519089148146107, 0.59171106814975671], [1.1252472995735809, 1.2722812742580845, 1.296157580183261]] N_DET: -0.860447181357 N_DET: -0.0603705511147 N_DET: -0.24839340451 NV: nan nan nan SNV: nan nan nan nan nan
原因究明
NaNとなってしまう原因はどこにあるのかを突き止めてみると、ガウス分布の計算内で分散行列の行列式を出すのですが、そこで負の値になってしまっているようでした。その値の平方根を取るものだから当然実数にはならず、NaNとなってしまったのです。なるほど。 そもそものこの共分散行列をかくにんしたところ、
{\displaystyle \Sigma } \Sigma は、半正定値行列
分散共分散行列 - Wikipedia
半正定値行列というのは、行列式が0か正の値になる行列のこと。ということはそもそも負の値が出てくること時点でおかしいということです。 よし、原因はつかめた。あとは訂正をするだけだ。。。ここからが長かった。
行列式のコーディングのチェック
問題となるのは以下の分散を求める部分のコード。意図的にNumpyの行列を使わず、理解のため分散、共分散をそれぞれ計算してみようということで以下のリスト内包表記のコードとなっています。
self.v = [[sum([(self.x[i]-self.nu[j][0])**2*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)], [sum([(self.y[i]-self.nu[j][1])**2*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)], [sum([(self.x[i]-self.nu[j][0])*(self.y[i]-self.nu[j][1])*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)]]
最初のsumと次のsumが2次元の要素それぞれの分散値を計算、最後のsumが共分散を計算しています。なんども確認して問題なさそうだったのですが、その結果が以下のように行列式をとると負の値がでてきてしまう。なぜだ。
#分散1、分散2、共分散、行列式(ad-bc)
2.81130077476 2.98745380559 3.04287337554 -0.860447181357
0.512661193631 0.565190891481 0.59171106815 -0.0603705511147
1.12524729957 1.27228127426 1.29615758018 -0.24839340451
入力値とかも確認してみましたがそもそも共分散行列の行列式が負になること自体が異常なので、やはりこのコードがおかしいんですよね。 で、最終的に別の本に書いてあるEMアルゴリズムをコーディングしてみて、その行列要素を出力してみることにしました。すると。。。
V: # Result of ML Book's code
2.69263977682 0.640353547689 1.26287084435 0.129398664238
2.95622008252 0.425917289351 1.08691249439 0.0777264738108
2.85750222648 0.516449549181 1.19418340666 0.0496817279099
V: # Result of my code
2.69263977682 2.95622008252 2.85750222648 -0.205283191105
0.640353547689 0.425917289351 0.516449549181 0.00601751040866
1.26287084435 1.08691249439 1.19418340666 -0.0534439092193
おおぅ、行列の転置が起きてしまっているようですね。なるほど、リスト内包表記の組み合わせが正しくないようです。基本的な考え方は間違っていないかったですが、こうした順序の認識がまちがっていて、かつ訂正することも難しい(なにが間違っているか理解できない)状況に陥っていました。
訂正
これを踏まえて以下のように訂正をおこなったところ、出力からNaNが出てこなくなりました。
#Corrected self.v = [[sum([(self.x[i]-self.nu[j][0])**2*gamma[i][j] for i in range(150)])/n_k[j], sum([(self.y[i]-self.nu[j][1])**2*gamma[i][j] for i in range(150)])/n_k[j], sum([(self.x[i]-self.nu[j][0])*(self.y[i]-self.nu[j][1])*gamma[i][j] for i in range(150)])/n_k[j]] for j in range(3)] #Wrong self.v = [[sum([(self.x[i]-self.nu[j][0])**2*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)], [sum([(self.y[i]-self.nu[j][1])**2*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)], [sum([(self.x[i]-self.nu[j][0])*(self.y[i]-self.nu[j][1])*gamma[i][j] for i in range(150)])/n_k[j] for j in range(3)]]
反省
基礎知識がたりないですね。でもまぁ、もともと基礎知識が薄い中でこうしてコケることは織り込み済みで、コケながら覚えていくしかないかと思ってます。今回学んだことをまとめるといかになります。
- 共分散行列は半正定値行列。行列式が負の値になることはない。
- リスト内包表記は便利だけど順番を間違えやすい。転置状態に注意。
それでは次回はようやく、「確率モデルによるクラスタリング」にいけるかと思います。

<はじパタ> 10.3 階層型クラスタリング (融合型)
K-平均法(10.2)を扱った前回に引き続きまして、クラスタリングの10章。今回は階層型、融合型というような表現がされている分類方法についてみていきたいと思います。
階層型クラスタリング
この融合型の方法は「定義」により距離的に近いとされる2つのクラスを一つのクラスとして融合することを繰り返していきます。今回は引き続きアヤメのデータを使いましたが、この場合はクラスは3つとなりますので、融合をすすめていき、最終的に3つのクラスに収束したら終わりとしました。
融合するための距離の4つの「定義」
融合にはクラス間の距離的な近さを計測します。はじパタでは距離の定義について以下の4つを紹介しています。
- 単連結法
2クラスに属する要素通しで最も近いもの通しをそのクラス間の近さと定義して、その値が小さいもの通しを融合していく方法
- 完全連結法
2クラスに属する要素通しで最も遠いもの通しをそのクラス間の近さと定義して、その値が小さいもの通しを融合していく方法
- 群平均法
クラスタ内のすべての要素の平均をとり、各クラスの平均値間の距離をクラスの近さと定義する。その値が小さいもの通しを融合していく方法
コーディングの際の考慮すべき点
アヤメデータは150の要素から成り立つのでそれぞれの要素の距離を示す行列を持つ必要があり、150 x 150のマトリックスとなります。さらにそのうち、上記の定義により近いと判断された2点が同じクラスタとされていきます。要素に番号を振り、融合された要素をリスト化していく形で、マトリックスが縮小(=クラスタ(リスト)内の要素が増えていく)ようにして、最終的に3つのクラスタになった時点で止めるようにしました。 最小値をもとめるコードの大部分は使いまわしが可能で、変更すべき点は、マトリックスのマージのプロセスのみとなりました。
実行結果
アヤメデータ4つの特性をそれぞれ2つずつ、計6通りのセットで確認しています。評価については10.2のK-平均法と同じく正解率とF値を出すようにしています。詳細はこちら。
=== sepal length (cm) === sepal width (cm) === *** Single Linkage Method * correctness -- 0.35333333333333333 * F-Value -- 0.502442878626 *** Complete Linkage Method * correctness -- 0.52 * F-Value -- 0.518563070642 *** Group Average Method * correctness -- 0.7133333333333334 * F-Value -- 0.741125961406 *** Ward Method * correctness -- 0.78 * F-Value -- 0.73182865776 === sepal length (cm) === petal length (cm) === *** Single Linkage Method * correctness -- 0.6733333333333333 * F-Value -- 0.763119756663 *** Complete Linkage Method * correctness -- 0.84 * F-Value -- 0.825008207203 *** Group Average Method * correctness -- 0.7466666666666667 * F-Value -- 0.758906000869 *** Ward Method * correctness -- 0.84 * F-Value -- 0.825008207203 === sepal length (cm) === petal width (cm) === *** Single Linkage Method * correctness -- 0.34 * F-Value -- 0.501625617698 *** Complete Linkage Method * correctness -- 0.5866666666666667 * F-Value -- 0.648999234975 *** Group Average Method * correctness -- 0.7066666666666667 * F-Value -- 0.745888252968 *** Ward Method * correctness -- 0.8266666666666667 * F-Value -- 0.806976194904 === sepal width (cm) === petal length (cm) === *** Single Linkage Method * correctness -- 0.66 * F-Value -- 0.760564623487 *** Complete Linkage Method * correctness -- 0.94 * F-Value -- 0.941265889017 *** Group Average Method * correctness -- 0.8733333333333333 * F-Value -- 0.863216837848 *** Ward Method * correctness -- 0.8666666666666667 * F-Value -- 0.854987973338 === sepal width (cm) === petal width (cm) === *** Single Linkage Method * correctness -- 0.66 * F-Value -- 0.760564623487 *** Complete Linkage Method * correctness -- 0.8066666666666666 * F-Value -- 0.738999798162 *** Group Average Method * correctness -- 0.66 * F-Value -- 0.760564623487 *** Ward Method * correctness -- 0.84 * F-Value -- 0.82020552181 === petal length (cm) === petal width (cm) === *** Single Linkage Method * correctness -- 0.6733333333333333 * F-Value -- 0.763119756663 *** Complete Linkage Method * correctness -- 0.96 * F-Value -- 0.960162654599 *** Group Average Method * correctness -- 0.96 * F-Value -- 0.960162654599 *** Ward Method * correctness -- 0.8933333333333333 * F-Value -- 0.887000529608
考察
全体的な傾向としては単連結法が比較して正解率が良くなく、ほかの方法はケースバイケースでしょうか。そのなかでもウォード法は安定して高い値がでているように見えます。
K-平均法の時と同じようにすべての特性を扱った4次元データでの精度を確認してみましたが、やはり特徴点が顕著となる2点を使ったデータのほうが精度が高いという結果になりました。
また、K-平均法のほうが精度は高いです。結構苦労してコーディングしたのに悲しい限り。アヤメデータ以外でのK-平均法よりよくなるケースがあるのか気になるところではあります。
ソースコード
いかJupyter notebook上で動くソースです。
from sklearn import datasets import matplotlib.pyplot as plt from collections import Counter #inline pyplot class ClastaringFusion(): def __init__(self): self.x = [] self.y = [] self.p = [] self.t = [] self.pt = [] self.num = [50, 50, 50] iris = datasets.load_iris() self.feature_names = iris.feature_names features = iris.data targets = iris.target self.dmatrix = np.array([]) def install_val(self,a=1,b=2): self.p = [a, b] self.x = features.T[self.p[0]] self.y = features.T[self.p[1]] self.t = targets self.distance() def distance(self, x=None, y=None): if x==None: x = self.x self.dmatrix = np.array([[np.sqrt((self.x[i] - self.x[j])**2 + (self.y[i] - self.y[j])**2 ) for i in range(150)] for j in range(150)]) #return np.array([[np.sqrt((i - j)**2 + (i - j)**2) for i in x] for j in y]) def comp_fusion(self, list1, list2, fm=0): def ave(lst): x_lst = [self.x[i] for i in lst] y_lst = [self.y[i] for i in lst] m_x = sum(x_lst)/len(x_lst) m_y = sum(y_lst)/len(y_lst) return sum([(x_lst[i] - m_x)**2 + (y_lst[i] - m_y)**2 for i in range(len(lst))]) if fm ==0: v = min([min([self.dmatrix[l1, l2] for l2 in list2]) for l1 in list1]) elif fm==1: v = max([max([self.dmatrix[l1, l2] for l2 in list2]) for l1 in list1]) elif fm==2: v = sum([sum([self.dmatrix[l1, l2] for l2 in list2]) for l1 in list1]) /(len(list1) * len(list2)) elif fm==3: v = ave(list1+list2) - (ave(list1) + ave(list2)) else: print("Error: Invalid number for Fusion Method") sys.exit(1) return v def fusion(self, fm=0, tree=None): ''' fm (fusion_method) 0: Single Linkage Method 1: Complete Linkage Method 2: Group Average Method 3: Ward Method ''' if tree==None: tree = [[i] for i in range(150)] dmtx = np.array([[self.comp_fusion(i, j, fm) for i in tree] for j in tree]) for i in range(dmtx.shape[0]): dmtx[i, i] = 100 val = np.argmin(dmtx) #print(val) #print(dmtx.shape) #print("D", dmtx[val//dmtx.shape[0], val%dmtx.shape[0]]) minval = np.array(np.where(dmtx==dmtx[val//dmtx.shape[0], val%dmtx.shape[0]])) ctree = [] checked = [] lgth = minval.shape[1] #print(minval) #print("lgth: ", lgth) for i in range(lgth): flag = True one = tree[minval[0][i]] two = tree[minval[1][i]] checked += (one + two) inc_num = [] #print("one+two", one, two) #print(" ctree ", ctree) if minval[0][i] != minval[1][i]: for j, t in enumerate(ctree): if set(t) & set(one) or set(t) & set(two): inc_num.append(j) #print(" ", inc_num, " ==== ", one, two) #print(" ", ctree) if len(inc_num) == 0: ctree.append(one+two) else: ctree[inc_num[0]] = list(set(one+two+ctree[inc_num[0]])) if len(inc_num) > 1: for n in inc_num: ctree[inc_num[0]] = list(set(ctree[inc_num[0]]+ctree[n])) for k, n in enumerate(inc_num[::-1]): if k == len(inc_num)-1: break ctree.pop(n) for i in tree: if not set(i) & set(checked): ctree.append(i) #print(ctree) test = [] for t in ctree: test += t missing = (set(range(150)) - set(test)) tomatch = (set(test) - set(range(150))) #print("Missing", missing) #print("Too Match", tomatch) return ctree def show_all_result(self): fm_string = [ "Single Linkage Method", "Complete Linkage Method", "Group Average Method", "Ward Method" ] for i, (a, b) in enumerate(itertools.combinations(range(4), 2)): print(" === ", self.feature_names[a], " === ", self.feature_names[b], " === ") self.install_val(a, b) #self.plot_map() for fm in range(4): tree = cf.fusion(fm) c = 0 while len(tree) > 3: #print("======") tree = cf.fusion(fm, tree) #print(len(tree)) #if len(tree) < 4: # break c += 1 crct, fv = cf.correct_rate(tree, False) print(" *** ", fm_string[fm]) print(" * correctness -- ", crct) print(" * F-Value -- ", fv) def correct_rate(self, tree, verbose=True): trees = [] crcts = 0.0 fvs = 0.0 for p in list(itertools.permutations(range(3))): pt_tree = [] for i in range(150): for j in range(3): if i in tree[j]: pt_tree.append(p.index(j)) break trees.append(pt_tree) #print("tree", pt_tree) cnt = np.array([[Counter(pt_tree[i*50:i*50+50])[j] for i in range(3)] for j in range(3)]) odr = [np.argmax([Counter(pt_tree[j*50:j*50+50])[i] for i in range(3)]) for j in range(3)] crct = [] crctnum = 0 for i in range(150): if i // 50 == pt_tree[i]: crctnum += 1 fv = 1.0 for i in range(3): x = np.count_nonzero(pt_tree[i*50:i*50+50] == odr[i]) z = np.count_nonzero(pt_tree[(i+1)%3*50:(i+1)%3*50+50] == odr[i]) + \ np.count_nonzero(pt_tree[(i+2)%3*50:(i+2)%3*50+50] == odr[i]) rec = x/50 pre = 50/(50+z) fv *= 2*rec*pre/(rec+pre) if crctnum > crcts: fvs = fv crcts = crctnum #print("crct", crctnum) if verbose: print("CORRECTNESS: ", crcts/150) print("F-Value : ", np.cbrt(fvs)) return crcts/150, np.cbrt(fvs) cf = ClastaringFusion() cf.install_val(1, 2) cf.distance() cf.show_all_result()
関連記事
<はじパタ> 10.2 K-平均法 おまけ
今回は以下の記事のおまけになります。
K-平均法はランダムにK個クラスタした平均値をとって、その平均値に近い距離にいる要素をそのクラスタに分類する、という試行を収束するまで繰り返すものでした。
じゃあ実際にその平均値は各試行ごとにどのように変化するのかというのをアニメーションでプロットしてみました。 それが以下です。四角いポイントが各色の平均値となり、繰り返しによるクラスタの変化を各ステップごとにアニメーションで示しています。
なるほど、最初にランダムにアサインされたデータから各テリトリーごとに収束していく様子が見やすくなりました。これは面白いですね。
ただ、ランダムでアクセスするので、以下のようにちょっとおかしな収束してしまうこともあるようです。特殊なパターンの収束をさけるために、試行は一回ではなく複数回やるのがよさそうです。
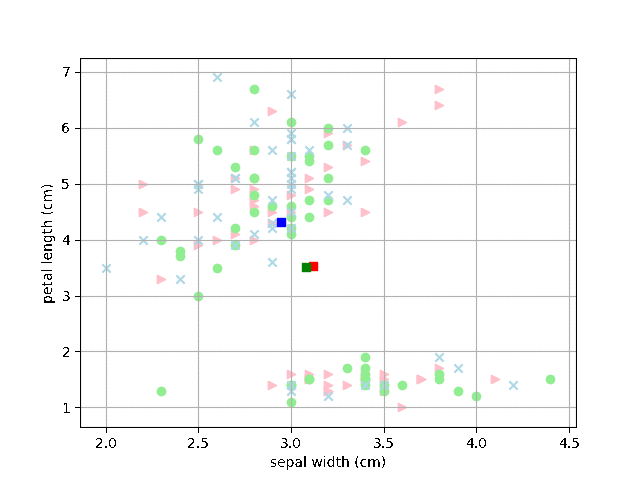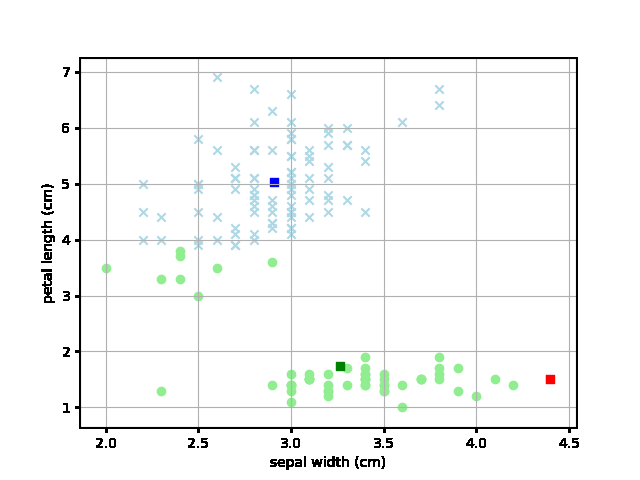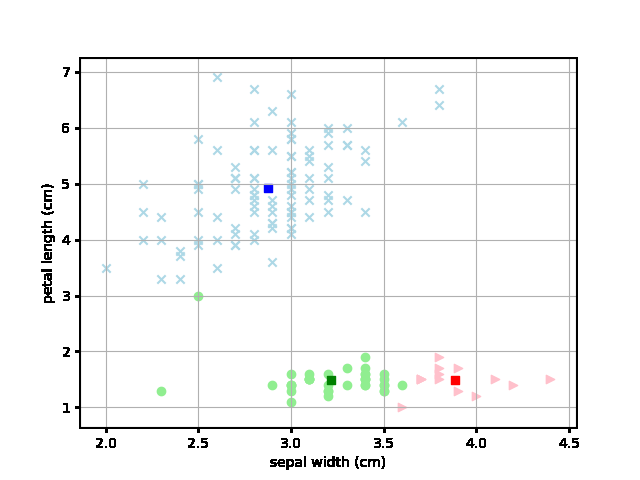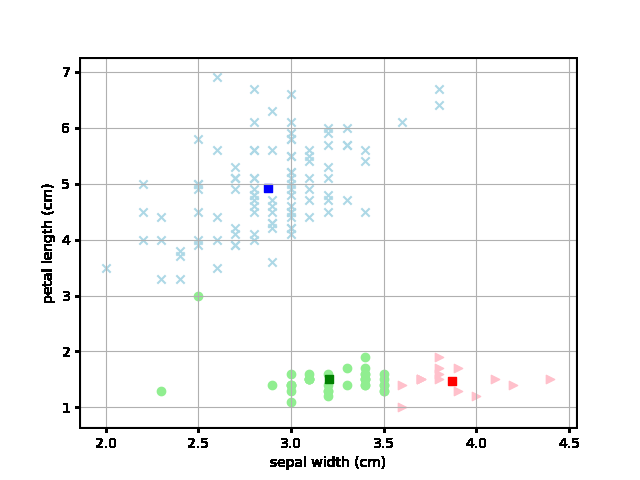
さて、次回は10.3融合法です。この方法もアヤメデータを使った分類をしてみて、その正確さを評価してみたいと思います。
<はじパタ> 10.2 非階層型クラスタリング (K-平均法)
いろいろごたごたしている中でも少しづつはじパタすすめておりまして、とりあえず10章のストックができたのでこちらの備忘録を掲載します。
10章はクラスタリングで教師データなしの状態でパターンニングをおこなう手法になります。定番のアヤメデータをこのK-平均法でクラスタリングをおこなうとどうなるかをスクリプトを書いてみてみました。
アヤメデータ
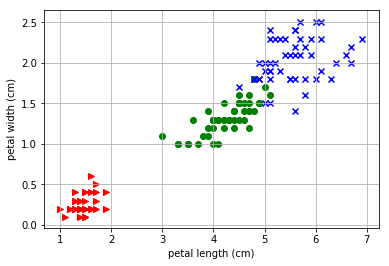
このアヤメデータは3種50セット、合計150個のアヤメそれぞれの特性(がく片の幅、がく片の長さ、弁の幅および 弁の長さ)を記載しています。
例えば、がく片の幅と弁の長さでデータをプロットした場合の2次元データは以下のプロットで表現できます。
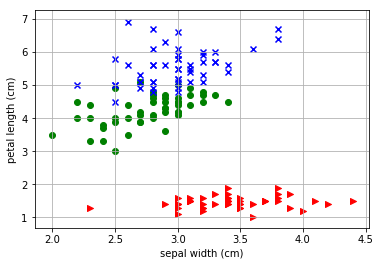
つまり、今回の問いはこの150個のデータを教師データなしでとりあえず3種区別してみる、というものになります。 アヤメデータのプロットのスクリプトは以下のサイトを参考にさせていただいています。
Python: Iris データセットを Matplotlib で可視化してみる | CUBE SUGAR STORAGE
今回のスクリプトについて
今回は視覚化しやすいように4つの特性から2つをとったデータについてK平均法を使って3つのクラスタに分けてみます。4つのデータから2つとるので、6種のデータとなります。さらに4つのデータ全部を使ってどう変化するかもみてみたいと思います。
評価方法
評価には2つの指標を使います。ひとつは正解率、もうひとつは精度と再現率を評価できるF値を求めます。以下のリンクが詳しいかと思います。
抑えておきたい評価指標「正解率」「精度」「再現率」 - HELLO CYBERNETICS
K平均法
K-平均法は最初にそれぞれの値のクラスタをランダムに決定します。今回は3個のアヤメデータなので3つのクラスタにわけます。そしてその3つのクラスタの平均値のポイントを求め、またそれぞれの値で一番距離が近い平均値のクラスタに変更し直します。これを繰り返してデータが更新されなくなったら終わりとするものです。
実行結果
がく片の幅と弁の長さの結果
まずは先ほども例として挙げた「がく片の幅」と「弁の長さ」についてK-平均法の結果をプロットしてしてみます。
- K-平均法の結果
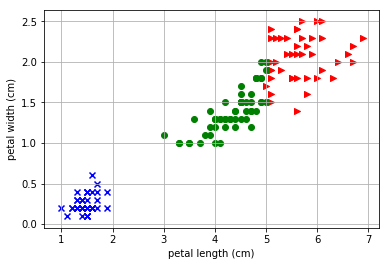
- 実際のデータ
- 評価値
=== sepal width (cm) , petal length (cm) === CORRECTNESS: 0.3867 , F-Value : 0.4761 CORRECTNESS: 0.94 , F-Value : 0.7417 CORRECTNESS: 0.8467 , F-Value : 0.8337 CORRECTNESS: 0.9 , F-Value : 0.897 CORRECTNESS: 0.9333 , F-Value : 0.9328 CORRECTNESS: 0.9533 , F-Value : 0.954 CORRECTNESS: 0.96 , F-Value : 0.9607 CORRECTNESS: 0.94 , F-Value : 0.9413 CORRECTNESS: 0.9267 , F-Value : 0.9271
もとのデータが比較的わかりやすく分かれていることもあるので、正答率もわるくないと思われます。ランダムにはじめて平均値とその距離でこうもきれいにわかれるものなのかと少し驚きました。3つの平均値をみてみると最初は3つとも近い場所にいるのですが、繰り返していくうちに平均的なポジションに落ち着く様子がわかりました。これも今度アニメーションでプロットしてみたいと思います。
また正解率やF値はピークを越えて少しだけ下がるところで収束してしまうようです。実際は回答とすべき教師データはないので、収束まつしか判断のしようがなさそうです。
4つの特性から2つピックアップしてみる
では、4つの特性から2つピックアップした時のそれぞれのK-平均法の評価値はどのように変わるか見てみましょう。初期値がランダムなので評価ごとに値は変更しますが、とりあえず評価値の大小関係は変わらないと考えてよいです。
=== sepal length (cm) , sepal width (cm) === CORRECTNESS: 0.4 , F-Value : 0.4831 CORRECTNESS: 0.7867 , F-Value : 0.689 CORRECTNESS: 0.8067 , F-Value : 0.8134 CORRECTNESS: 0.8267 , F-Value : 0.8363 CORRECTNESS: 0.82 , F-Value : 0.8306 === sepal length (cm) , petal length (cm) === CORRECTNESS: 0.3867 , F-Value : 0.4652 CORRECTNESS: 0.8267 , F-Value : 0.7216 CORRECTNESS: 0.88 , F-Value : 0.8794 CORRECTNESS: 0.9 , F-Value : 0.9021 CORRECTNESS: 0.8867 , F-Value : 0.8918 CORRECTNESS: 0.88 , F-Value : 0.885 CORRECTNESS: 0.8867 , F-Value : 0.8897 CORRECTNESS: 0.88 , F-Value : 0.8824 === sepal length (cm) , petal width (cm) === CORRECTNESS: 0.3667 , F-Value : 0.4585 CORRECTNESS: 0.8333 , F-Value : 0.6973 CORRECTNESS: 0.8267 , F-Value : 0.83 CORRECTNESS: 0.8267 , F-Value : 0.8352 CORRECTNESS: 0.8333 , F-Value : 0.8414 === sepal width (cm) , petal length (cm) === CORRECTNESS: 0.3867 , F-Value : 0.4761 CORRECTNESS: 0.94 , F-Value : 0.7417 CORRECTNESS: 0.8467 , F-Value : 0.8337 CORRECTNESS: 0.9 , F-Value : 0.897 CORRECTNESS: 0.9333 , F-Value : 0.9328 CORRECTNESS: 0.9533 , F-Value : 0.954 CORRECTNESS: 0.96 , F-Value : 0.9607 CORRECTNESS: 0.94 , F-Value : 0.9413 CORRECTNESS: 0.9267 , F-Value : 0.9271 === sepal width (cm) , petal width (cm) === CORRECTNESS: 0.3933 , F-Value : 0.4796 CORRECTNESS: 0.9533 , F-Value : 0.7596 CORRECTNESS: 0.86 , F-Value : 0.7473 CORRECTNESS: 0.8467 , F-Value : 0.841 CORRECTNESS: 0.8733 , F-Value : 0.876 CORRECTNESS: 0.8933 , F-Value : 0.8965 CORRECTNESS: 0.9133 , F-Value : 0.9168 CORRECTNESS: 0.9267 , F-Value : 0.9293 CORRECTNESS: 0.9267 , F-Value : 0.9292 === petal length (cm) , petal width (cm) === CORRECTNESS: 0.36 , F-Value : 0.4523 CORRECTNESS: 0.9467 , F-Value : 0.7468 CORRECTNESS: 0.8467 , F-Value : 0.8292 CORRECTNESS: 0.9267 , F-Value : 0.9258 CORRECTNESS: 0.96 , F-Value : 0.9602 CORRECTNESS: 0.9733 , F-Value : 0.9735 CORRECTNESS: 0.9667 , F-Value : 0.9672 CORRECTNESS: 0.96 , F-Value : 0.9606
概ね、0.85~0.95といったあたりに収まるでしょうか。
4つの特性を使った評価
では、2つといわず一気に4つの特性を使った4次元での評価はどうなるか確認をしてみたいと思います。
CORRECTNESS: 0.4267 , F-Value : 0.5037 CORRECTNESS: 0.8467 , F-Value : 0.7439 CORRECTNESS: 0.8667 , F-Value : 0.8586 CORRECTNESS: 0.9 , F-Value : 0.897 CORRECTNESS: 0.9 , F-Value : 0.9007 CORRECTNESS: 0.92 , F-Value : 0.9221 CORRECTNESS: 0.92 , F-Value : 0.9227 CORRECTNESS: 0.9067 , F-Value : 0.9096 CORRECTNESS: 0.9 , F-Value : 0.9021 CORRECTNESS: 0.8933 , F-Value : 0.8937 CORRECTNESS: 0.8867 , F-Value : 0.8866
あれれ、精度としては特徴がよく表れている2つをピックアップしたほうがよい数値がでているようにもみえます。でもおそらく、その結果はその特徴量に強く適合がしすぎてしまっているかと思われるので、こちらの4次元での方法はより「一般的」「総合的」な評価がしやすくなるのかとは思います。
ソースコード
今回利用したソースコードです。Jupyter notebook上で動作を確認しており、 processで実行、2つの引数はアヤメの4つ特性 0~3のうち2つピックするのと、3つ目の引数はプロットをするかTrue/Falseで表しています。
import numpy as np from sklearn import datasets import matplotlib.pyplot as plt from collections import Counter #inline pyplot class Iris_PM: def __init__(self): self.p = [2, 3] self.x = [] self.y = [] self.t = [] self.pt = [] self.num = [50, 50, 50] iris = datasets.load_iris() features = iris.data targets = iris.target def install(self, a=2, b=3): self.x = features.T[a] self.y = features.T[b] self.t = targets def plot_map(self, df=False): p = self.pt if df: p = self.t for t, marker, c in zip(range(3), '>ox', 'rgb'): plt.scatter( #self.x[50*t:50*t+49], #self.y[50*t:50*t+49], features[p == t, self.p[0]], features[p == t, self.p[1]], marker=marker, c=c, ) plt.xlim(1.9, 4.5) plt.ylim(0.9, 7.1) plt.xlabel(feature_names[self.p[0]]) plt.ylabel(feature_names[self.p[1]]) plt.autoscale() plt.grid() #print(linear_pro(w, np.array([1.,1.,1.]))) plt.show() def randomize(self): self.pt = np.array([np.random.randint(3) for i in range(sum(self.num))]) def means(self): nu = [[0.0, 0.0], [0.0, 0.0], [0.0, 0.0]] cnt = [0, 0, 0] for i in range(sum(self.num)): nu[krs.pt[i]][0] += self.x[i] nu[krs.pt[i]][1] += self.y[i] cnt[krs.pt[i]] += 1 for i in range(3): nu[i][0] /= cnt[i] nu[i][1] /= cnt[i] return nu def correct_rate(self): #print(self.pt) cnt = np.array([[Counter(self.pt[i*50:i*50+50])[j] for i in range(3)] for j in range(3)]) #print(cnt) #print([np.argmax([Counter(self.pt[j*50:j*50+50])[i] for i in range(3)]) for j in range(3)]) #print([np.argmax([Counter(self.pt[i*50:i*50+50])[j] for i in range(3)]) for j in range(3)]) odr = [np.argmax([Counter(self.pt[j*50:j*50+50])[i] for i in range(3)]) for j in range(3)] lodr = [] for i in odr: lodr += ([i]*50) fv = 1.0 for i in range(3): x = np.count_nonzero(self.pt[i*50:i*50+50] == odr[i]) z = np.count_nonzero(self.pt[(i+1)%3*50:(i+1)%3*50+50] == odr[i]) + \ np.count_nonzero(self.pt[(i+2)%3*50:(i+2)%3*50+50] == odr[i]) rec = x/50 pre = 50/(50+z) fv *= 2*rec*pre/(rec+pre) print("CORRECTNESS: ", "{:.4}".format(np.sum(self.pt == lodr)/150), ",\t F-Value : ", "{:.4}".format(np.cbrt(fv))) def process(self, a=1, b=2, plot_map=False): self.install(a,b) self.randomize() bak_list = [] cnt = 0 print(" === ", feature_names[a], ", ", feature_names[b]," === ") while self.pt is not bak_list and cnt < 30: self.correct_rate() cnt += 1 bak_list = self.pt nu = self.means() up = [] #krs.plot_map() for i in range(sum(self.num)): #print(n,":", krs.x[i], krs.y[i], nu) up.append(np.argmin([[(self.x[i]-n[0])**2 + (self.y[i]-n[1])**2 for n in nu]])) self.pt = np.array(up) nu = self.means() if np.allclose(bak_list, self.pt): if plot_map: self.plot_map() self.plot_map(True) break print("") krs = Iris_PM() krs.process(1,2,False)