異常検知と変化検知 - 第3章 k近傍法

モチベーション

異常検知と変化検知 (機械学習プロフェッショナルシリーズ)

この本読み始めました。専門知識とか、数学の基礎知識が多く私が理解するにはちょっとハードルが高めだったのですが、Pythonで可視化して、どのようなアルゴリズムなのかを理解しながらゆっくり進めたいと思います。このエントリーでは 3章の「近傍法による異常検知」から k近傍法を可視化したうえで方法を説明できればと思っています。 アルゴリズムの詳細をかききるのは難しいかと思いますので、気になった方は本を参照いただければと思います。

k近傍法のサマリ

簡単な例として、異常と正常のラベルがついた (x, y) の二次元のサンプルがあるとします。サンプルそれぞれの点から k 個の近い点をチェックしてその正常値、異常値が含まれる割合を求めて、異常値と判断する割合の閾値を計算します。その後、新しい値が来たときに同じような割合の計算をして設定した閾値を超える場合はAlertを出すようにします。

詳細は本書と、外部ですが以下のスライドがわかりやすいかと思います。 異常検知と変化検知 第4章 近傍法による異常検知

今回は正規分布をランダムにだす numpy の関数 randn() を使ってサンプル値を作成します。

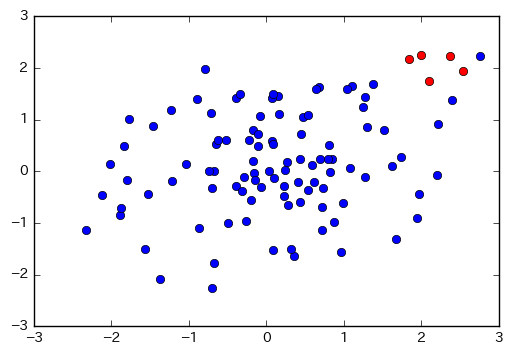
num = 100 # 正常値の数
inum = 5 # 異常値の数
# randn()で正常値を 100個、異常値を中心をずらして5個　設定
smpl = [[randn(), randn(), 0] for i in range(num)]
smpl += [[randn()*0.4 + 2.0, randn()*0.4 + 2.0, 1] for i in range(inum)]

図示すると以下のようになります。

参照数 k と 閾値 F値 をサンプルより計算する

少し驚いたのですが、サンプルから最適な参照する近傍数kと閾値であるF値が高くなるa_thの値を変更しながら一番最適な閾値を見つけるのが事前にやる作業になります。これが経験分布ってことで正しいのでしょうか。そのあたりわかっていません。

kの候補の値を１～６まで、a_thの候補の値を0~5まで0.1まで細かく確認して、F値を計算します。

        klist = [1, 2, 3, 4, 5, 6]
        athlist = [0.1*(1+i) for i in range(50)]
        # 現在までの最大値を記録 [k値、a_thの値、最終的な閾値F値]
        maxset = [0, 0, 0.0]
        for kv in klist:
            for av in athlist:
                self.k = kv
                self.ath = av
                tmp_set = [kv,av,self.calc_ath()]
                #print "k, ath, f", tmp_set
                if tmp_set[2] >= maxset[2]:
                    maxset = list(tmp_set)

閾値を比較するためにのF値の計算は calc_ath()の関数で計算します。F値に関しては一章に書かれてますので、ご参照いただければと思います。

k 値と a_thの値から導き出された F値をプロットしてみます。 ちょっとわかりずらいからと思いますが、k=4の時のF値が 0.3636…と一番高い値になります。このF値が基準として、異常値の判定をおこないます。

F値が超える範囲にいろをつけてみた

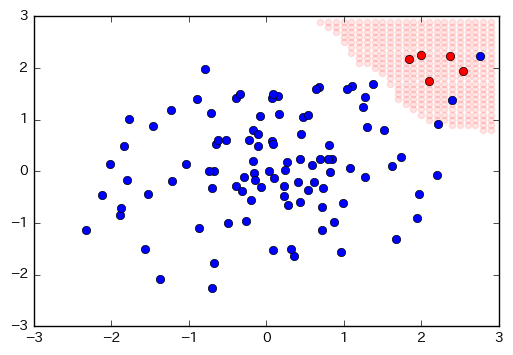
参照する近傍数K=4で設定して、0.3636を超える場所を薄赤で表示してみます。

    def plot_abn(self):
        k, ath = self.check_better_comb()
        print k, ath
        xl = []
        yl = []
        
        # 縦横-3.0 から 3.0まで0.1でF値を計算してプロット
        for x in range(60):
            xd = x*0.1 - 3.0
            for y in range(60):
                yd = y*0.1 - 3.0
                dltList = []
                # 各地点とサンプル間の距離を計算
                for j, smp in enumerate(self.smpl):
                    dltList.append([self.delta(smp[0:2], [xd, yd]), j])

                nml, abnml = 0, 0
                n_cor, ab_cor = 0, 0
                # 近い順に k 個のサンプルを抽出してF値を算出。
                # 閾値を超えた値をxl, ylに記録
                for j, dl in enumerate( sorted(dltList)):
                    if j == k:
                        break

                    if self.smpl[dl[1]][2] == 1:
                        abnml += 1
                    else:
                        nml += 1

                if np.log(self.pi0*abnml)-np.log(self.pi1*nml) > ath:
                    xl.append(xd)
                    yl.append(yd)

        plt.xlim(-3.0, 3.0)
        plt.ylim(-3.0, 3.0)
        plt.scatter(xl, yl, color='r', alpha=0.1)
        self.ploting()
        plt.show()

表示すると以下のようになります。異常値である赤の周りが異常値として判定されるいるのがわかります。多少正常値のサンプルも入ってきますが、アラートを上げる範囲としては妥当といえるかと思います。

ソースコード

以下、今回利用したソースコードになります。ご確認を

import numpy as np
import matplotlib.pyplot as plt
import random
from numpy.random import *
%matplotlib inline

num = 100
inum = 5
smpl = [[randn(), randn(), 0] for i in range(num)]
smpl += [[randn()*0.4 + 2.0, randn()*0.4 + 2.0, 1] for i in range(inum)]

class KNearest():
    def __init__(self):

        self.num = num
        self.inum = inum

        self.pi0 = self.num*1.0/(self.num+self.inum)
        self.pi1 = self.inum*1.0/(self.num+self.inum)
        
        self.k = 5
        self.ath = 0.1
        self.cand = []
        
        self.smpl = smpl

    # サンプルのPlot
    def ploting(self):
        plt.xlim(-3.0, 3.0)
        plt.ylim(-3.0, 3.0)
        for s in self.smpl:

            if s[2] == 0:
                plt.plot(s[0], s[1], 'bo')
            else:
                plt.plot(s[0], s[1], 'ro')

    # 2地点の距離の計算
    def delta(self, a, b):
        return (a[0]-b[0])**2 + (a[1]-b[1])**2

    # a_thからF値計算。。。データ消してしまった　orz..後ほど
    def calc_ath(self):

    # 最適なF値の計算
    def check_better_comb(self):
        klist = [1, 2, 3, 4, 5, 6]
        athlist = [0.1*(1+i) for i in range(50)]
        
        maxset = [0, 0, 0.0]
        for kv in klist:
            for av in athlist:
                self.k = kv
                self.ath = av
                tmp_set = [kv,av,self.calc_ath()]
                #print "k, ath, f", tmp_set
                if tmp_set[2] >= maxset[2]:
                    maxset = list(tmp_set)

        return maxset[0], maxset[2]

    # F値のプロット
    def plot_better_comb(self):
        klist = [1, 2, 3, 4, 5, 6]
        athlist = [0.1*(1+i) for i in range(50)]
        
        result = {}
        maxset = [0, 0, 0.0]
        for kv in klist:
            result[kv] = []
            for av in athlist:
                self.k = kv
                self.ath = av
                result[kv].append(self.calc_ath())

        for kv in klist:
            plt.plot(athlist, result[kv], label='k =' + str(kv))
        plt.legend()
    
    # F値を超越して異常と判定される範囲をプロット
    def plot_abn(self):
        k, ath = self.check_better_comb()
        print k, ath
        xl = []
        yl = []
        
        
        for x in range(60):
            
            xd = x*0.1 - 3.0
            for y in range(60):
                yd = y*0.1 - 3.0
                dltList = []
                for j, smp in enumerate(self.smpl):
                    dltList.append([self.delta(smp[0:2], [xd, yd]), j])

                nml, abnml = 0, 0
                n_cor, ab_cor = 0, 0
                for j, dl in enumerate( sorted(dltList)):
                    if j == k:
                        break

                    if self.smpl[dl[1]][2] == 1:
                        abnml += 1
                    else:
                        nml += 1

                if np.log(self.pi0*abnml)-np.log(self.pi1*nml) > ath:
                    #print xd, yd
                    xl.append(xd)
                    yl.append(yd)

        plt.xlim(-3.0, 3.0)
        plt.ylim(-3.0, 3.0)
        plt.scatter(xl, yl, color='r', alpha=0.1)
        self.ploting()
        plt.show()